|
Prediction of Wettability between
Liquid Metals and Covalent Ceramics
L.Zoltai
LIMOS R&D, Department of Physical Chemistry,
Faculty of Materials and Metallurgical Engineering, University of Miskolc,
3515 Hungary, Miskolc, Egyetemvaros
|
Abstract
Contact angle values have been estimated by the model developed by us earlier for 48 * 6 = 288 liquid metal / covalent ceramic
systems. 130 systems can be taken as ‘non-reactive’, i.e. the calculated value in this paper is expected to be an equilibrium
value, being independent of contact time. In 158 systems some chemical reaction or mutual solubility in the system is
expected, and so the calculated values will be valid in reality only during short contact
times. The calculated contact angle values vary within a relatively small
interval, ranging from 143o for the Li/B4C system to 170o for the
Pd/b
-SiC system. For the given liquid metal, the contact angle increases gradually in the following
row: B4C à
Si3N4 à
b
-BN à
AlN à
a
-BN à
b
-SiC. The range of contact angle for one given metal decreases with the increasing average value of the contact
angle. For Li, with a highest polarising effect the contact angle varies in the interval of 10o, while for Pd this interval is only 4o. The effect of temperature has been found negligible in all systems
(changing in the interval between +1o and –3o while the temperature changes by 100 K). It has been
concluded, that due to high surface tension of liquid metals, in absence of chemical interaction and mutual solubility between them and covalent
ceramics, liquid metals never wet the surface of covalent ceramics better than 143o.
Keywords:
wettability, contact angle, adhesion energy, model calculation, liquid
metals, B4C,Si3N4, b
-BN, AlN, a
-BN, b
-SiC. |
1. Introduction
Metals and ceramics interact with each other during innumerable engineering problems and manufacturing processes such as foundry
processes, composite production etc., thus the knowledge of adhesion energy and contact angle between these phases can be very
useful. A relatively large experimental databank on the contact angle between liquid metals and ceramics is available now in the literature [1-5]. In addition to
that, in recent years our research group have completed a large number of experiments on determination of the contact angle in different
metal/ceramic systems, including measurements on a covalently bonded Si3N4 ceramic [6-7]. Based on literature data and our own
measurements, a complete adhesion theory was developed by us on the liquid metal – covalent ceramic systems [8].
The goal of the present paper is to apply the model developed in [8] to calculate the contact angle values in 48 * 6 = 288 liquid
metal/covalent ceramic systems. It should be noted, however, that some of the possible combinations are ‘reactive
systems’, meaning that chemical reaction or mutual solubility can take place between the
phases. Therefore, in reactive systems our calculated results will be only ‘initial’
values, corresponding to short contact times between the phases (see [2, 9]). In ‘non-reactive’ systems our calculated results will refer to the equilibrium contact angle
values, being valid independent of the duration of contact between the two
phases.
2. Short summary of the model [8]
The model is based on the London-van-der-Waals
equation, as between covalent ceramics and liquid metals no other interaction can be
envisioned. For the interaction of a pure metal with a multi-component ceramics AxBy, summation should be performed over the tow components of the
ceramics. The final equation for the adhesion energy between the liquid metal and non-reactive covalent ceramic phase was derived
as:
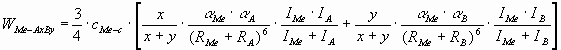 (1) (1)
where W - adhesion energy (J/m2),
a
- polarizability (m3),
I - first ionisation potential
(J/mol),
R - radius of atom (m),
indexes Me, C and i refer to liquid metal, ceramics and to the ith component of the
ceramic, respectively,
cMe-c - the number of bonds per unit interface area
(mol/m2):
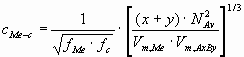 (2) (2)
where NAv - is the Avogadro number (6.02 1023mol-1),
Vm - is the molar volume (m3/mol),
f - is the correction factor, being the function of the volume- and surface occupancy
factors.
The contact angle can be calculated from the Young-Dupré
equation:
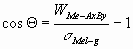 (3) (3)
where s
Mel-g is the surface tension of the liquid metal (J/m2).
3. Selection of Physical Constants [8]
In order to apply Eq.(1) for the estimation of the adhesion energy in the liquid metal – covalent ceramic
systems, first parameters used in Eq-s. (1-3) should be defined. The molar volume of liquid metals is taken from the compilation [10]. The molar volume of ceramics is taken from [21]. The packing factor fMe for liquid metals is taken equal 1.06 [20]. For the hexagonal and cubic ceramics fc is estimated as 1.09.
The polarizability of the atom at the surface of the liquid metal was estimated as the 1/6th part of the polarizability of the gaseous atom:
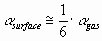 (4) (4)
Data of polarizability of gaseous atoms are taken from [13-14]. As follows from [13], the polarizability of covalent gaseous molecules can be approximately calculated additively from their atomic
polarizabilities. Therefore Eq.(4) will also be applied to the components of the covalent
ceramic.
The ionization potential of a metallic atom in the surface of the liquid metal can be approximately calculated
as:
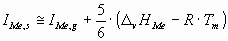 (5) (5)
where D
vHMe is the vaporization enthalpy of the liquid metal at its melting point
(Tm) [17],
R = 8.314 J/molK – the gas constant,
IMe,g – the first ionization energies of the gas atoms are taken from [12],
coefficient 5/6 refers to the fact that the cohesion energy of the surface atom is
approximately the 5/6th part of the cohesion energy of the bulk atom.
The ionization potential of different components of the ceramic should be estimated in different
ways, depending on, whether they are solid or gaseous as a pure phase under standard
conditions. As an example, in case of the Si3N4 ceramics, silicon is
solid, while nitrogen is two-atomic gas in standard state. Therefore, for the two components of Si3N4 the ionization energies should be estimated in slightly different
ways:
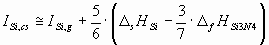 (6.a) (6.a)
 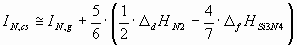 (6.b) (6.b)
where D
sHSi is the sublimation enthalpy of Si [17],
D
fHSi3N4 is the enthalpy of formation of Si3N4 [17],
D
dHN2 is the enthalpy of dissociation of 1 mol of N2(g) into 2 moles of
N(g) [17].
The radii for liquid metals are taken from the table for atomic
(metallic) radii (coordination: 12) from [18]. The radii of the components of the ceramic is estimated from the smallest distance between the components in the
compound, taking into account their radii in pure state. As an example, the smallest distance between Si and N in the Si3N4 compound is 1.71 10-10 m [11]. Using the metallic radius of Si (1.34 10-10 m [18]) and orbital radius of gaseous nitrogen (0.521 10-10 m [18]), the radii of the components of the ceramics were taken
as: RSi = 1.23 10-10 m, RN = 0.478 10-10 m.
In Tables 1-2 the initial physical data are summarised for the metals and
ceramics, respectively.
Table 1. Physical parameters of metals needed for calculations
|
Me |
Tm [
17]
|
Vm at Tm[
10]
|
a
[
10]
|
f [
20]
|
a(gas) [
13]
|
I(gas) [
12]
|
DvH at Tm[
17]
|
R[
18]
|
slg at Tm[
20]
|
dslg/
dT[
20]
|
|
K |
e-6, m3/mol |
10-4 K-1 |
|
e-30, m3 |
kJ/mol |
kJ/mol |
e-10, m |
mJ/m2 |
mJ/m2K |
|
Li |
453.69 |
13.4 |
1.9 |
1.06 |
24.3 |
513.3 |
155.3 |
1.55 |
470 |
-0.2 |
|
Na |
370.98 |
24.8 |
2.54 |
1.06 |
23.6 |
495.8 |
104.1 |
1.89 |
190 |
-0.13 |
|
K |
336.35 |
47.1 |
2.9 |
1.06 |
43.4 |
418.8 |
86.3 |
2.36 |
100 |
-0.08 |
|
Rb |
312.65 |
57.7 |
3 |
1.06 |
47.3 |
403 |
78.6 |
2.48 |
86 |
-0.07 |
|
Cs |
301.55 |
72.2 |
3.1 |
1.06 |
59.6 |
375.7 |
74.4 |
2.67 |
69 |
-0.06 |
|
Be |
1560 |
5.33 |
0.71 |
1.06 |
5.6 |
899.4 |
309.1 |
1.13 |
1300 |
-0.31 |
|
Mg |
922 |
15.3 |
1.6 |
1.06 |
10.6 |
737.7 |
132.6 |
1.6 |
590 |
-0.19 |
|
Ca |
1112 |
29.5 |
1.6 |
1.06 |
23.9 |
589.7 |
159.1 |
1.97 |
370 |
-0.12 |
|
Sr |
1050 |
37 |
1.1 |
1.06 |
27.6 |
549.5 |
146.3 |
2.15 |
300 |
-0.11 |
|
Ba |
1002 |
41.4 |
0.81 |
1.06 |
39.7 |
502.8 |
160.9 |
2.21 |
280 |
-0.11 |
|
Al |
933.45 |
11.3 |
1.5 |
1.06 |
6.8 |
577.4 |
314.2 |
1.43 |
950 |
-0.26 |
|
Ga |
302.8 |
11.4 |
0.92 |
1.06 |
8.12 |
578.8 |
266.2 |
1.39 |
715 |
-0.088 |
|
In |
429.76 |
16.3 |
0.97 |
1.06 |
9.6 |
558.3 |
238.2 |
1.66 |
565 |
-0.09 |
|
Tl |
577 |
18 |
1.15 |
1.06 |
7.55 |
589.3 |
174.2 |
1.71 |
460 |
-0.1 |
|
Si |
1685 |
11.1 |
1.4 |
1.06 |
5.38 |
786.5 |
393.2 |
1.34 |
830 |
-0.084 |
|
Ge |
1210.4 |
13.2 |
0.89 |
1.06 |
6.07 |
762.1 |
339.1 |
1.39 |
610 |
-0.11 |
|
Sn |
505.06 |
17 |
0.87 |
1.06 |
7.7 |
708.2 |
292.7 |
1.58 |
550 |
-0.076 |
|
Pb |
600.6 |
19.42 |
1.24 |
1.06 |
6.8 |
715.9 |
188.1 |
1.75 |
455 |
-0.085 |
|
Sb |
904 |
18.8 |
1.3 |
1.06 |
6.6 |
833.6 |
240.6 |
1.61 |
380 |
-0.07 |
|
Bi |
544.52 |
20.8 |
1.17 |
1.06 |
7.4 |
703.3 |
196.6 |
1.82 |
385 |
-0.077 |
|
Cu |
1358 |
7.94 |
1 |
1.06 |
6.7 |
745.4 |
316.9 |
1.28 |
1350 |
-0.3 |
|
Ag |
1233.95 |
11.6 |
0.98 |
1.06 |
7.88 |
731 |
265.8 |
1.44 |
920 |
-0.24 |
|
Au |
1337.58 |
11.3 |
0.835 |
1.06 |
6.14 |
890.1 |
348.2 |
1.44 |
1140 |
-0.23 |
|
Zn |
692.65 |
9.94 |
1.5 |
1.06 |
6.3 |
906 |
120.5 |
1.36 |
820 |
-0.27 |
|
Cd |
594 |
14 |
1.5 |
1.06 |
7.2 |
867.6 |
103.6 |
1.56 |
630 |
-0.2 |
|
Hg |
234.29 |
14.65 |
1.77 |
1.06 |
5.4 |
1007 |
61.83 |
1.6 |
500 |
-0.19 |
|
La |
1193 |
23.3 |
0.4 |
1.06 |
31.1 |
538.1 |
419 |
1.87 |
750 |
-0.1 |
|
Ti |
1939 |
11.6 |
0.56 |
1.06 |
14.6 |
658 |
441.2 |
1.46 |
1600 |
-0.35 |
|
Zr |
2125 |
15.4 |
0.54 |
1.06 |
17.9 |
660 |
579.6 |
1.6 |
1500 |
-0.29 |
|
Hf |
2500 |
14.9 |
0.53 |
1.06 |
16.2 |
642 |
575.7 |
1.59 |
1500 |
-0.24 |
|
V |
2175 |
9.5 |
0.6 |
1.06 |
12.4 |
650 |
457.5 |
1.34 |
1900 |
-0.29 |
|
Nb |
2740 |
11.9 |
0.51 |
1.06 |
15.7 |
664 |
685.2 |
1.45 |
2100 |
-0.21 |
|
Ta |
3287 |
12.1 |
0.46 |
1.06 |
13.1 |
761 |
748.3 |
1.46 |
2200 |
-0.19 |
|
Cr |
2130 |
8.27 |
1.1 |
1.06 |
11.6 |
652.7 |
353.6 |
1.27 |
1700 |
-0.35 |
|
Mo |
2897 |
10.3 |
0.53 |
1.06 |
12.8 |
685 |
585.9 |
1.39 |
2300 |
-0.32 |
|
W |
3680 |
10.5 |
0.45 |
1.06 |
11.1 |
770 |
808.9 |
1.4 |
2500 |
-0.25 |
|
Mn |
1517 |
9.54 |
1.6 |
1.06 |
9.4 |
717.4 |
246.7 |
1.3 |
1200 |
-0.38 |
|
Re |
3453 |
9.96 |
0.44 |
1.06 |
9.7 |
760 |
706.7 |
1.37 |
2800 |
-0.3 |
|
Fe |
1809 |
7.94 |
1.3 |
1.06 |
8.4 |
759.3 |
378 |
1.26 |
1900 |
-0.42 |
|
Ru |
2523 |
9.27 |
- |
1.06 |
9.6 |
711 |
614.5 |
1.33 |
2300 |
-0.31 |
|
Os |
3300 |
9.46 |
- |
1.06 |
8.5 |
840 |
747.5 |
1.35 |
2500 |
-0.25 |
|
Co |
1768 |
7.6 |
1.4 |
1.06 |
7.5 |
760 |
396.6 |
1.25 |
1900 |
-0.4 |
|
Rh |
2233 |
9.27 |
- |
1.06 |
8.6 |
720 |
517.4 |
1.34 |
2000 |
-0.34 |
|
Ir |
2716 |
9.61 |
- |
1.06 |
7.6 |
880 |
625.7 |
1.36 |
2300 |
-0.32 |
|
Ni |
1726 |
7.43 |
1.51 |
1.06 |
6.8 |
736.7 |
399.9 |
1.24 |
1800 |
-0.44 |
|
Pd |
1825 |
10.14 |
1.17 |
1.06 |
4.8 |
805 |
348.5 |
1.37 |
1500 |
-0.26 |
|
Pt |
2045 |
10.31 |
1.52 |
1.06 |
6.5 |
870 |
533.3 |
1.38 |
1750 |
-0.36 |
Table 2. Physical parameters of ceramics needed for calculations
|
Ceramics |
Si3N4 |
b
-SiC |
B4C |
AlN |
a
-BN |
b
-BN |
|
Structure |
hex |
cub |
trig |
hex |
hex |
cub |
|
Vm, 293 K [
21]
|
e-6, m3/mol |
44 |
12.5 |
21.95 |
12.53 |
10.84 |
7.2 |
|
b [
21]
|
e-6, 1/K |
8.25 |
14.1 |
13.5 |
15 |
3.3 |
- |
|
a
(gas, A) [
13]
|
e-30,m3 |
5.38 |
5.38 |
3.03 |
6.8 |
3.03 |
3.03 |
|
a
(gas, B) [
13]
|
e-30,m3 |
1.1 |
1.76 |
1.76 |
1.1 |
1.1 |
1.1 |
|
Dist(A-B) [
11]
|
e-10, m |
1.715 |
2.2 |
1.63 |
1.885 |
1.58 |
1.567 |
|
R(A, met) [
18]
|
e-10, m |
1.34 |
1.34 |
0.91 |
1.43 |
0.91 |
0.91 |
|
R(B, orb) [
18]
|
e-10, m |
0.521 |
0.62 |
0.62 |
0.521 |
0.521 |
0.521 |
|
I(A, gas) [
12]
|
kJ/mol |
786.5 |
786.5 |
800.6 |
577.4 |
800.6 |
800.6 |
|
I(B, gas) [
12]
|
kJ/mol |
1402.3 |
1086.2 |
1086.2 |
1402.3 |
1402.3 |
1402.3 |
|
DsHA298K [
17]
|
kJ/mol |
450 |
450 |
560 |
329.7 |
560 |
560 |
|
DfH(AxBy)298K [
17]
|
kJ/mol |
-744.8 |
-73.22 |
-71.13 |
-317.98 |
-254.39 |
-254.39 |
|
DdH(B2)298K [
17]
|
kJ/mol |
945.4 |
0 |
0 |
945.4 |
945.4 |
945.4 |
Results of calculations
The results of calculations are summarized in Table 3 for 48 * 6 = 288 systems. In the first column the symbol of the metallic element, while in following six double columns the calculated values are given for the 6 different ceramics. In each double column first the calculated contact angle is given. After that, the category of this calculated result is marked by ‘eq.’ or ‘init.’. These two categories have been defined in this paper as follows:
-
‘eq.’: meaning that the calculated value is an equilibrium contact angle, taking place independent of the contact time in the ceramic/liquid metal system; this category was chosen, when the liquid metal has no chemical interaction (with negative standard change of Gibbs energy of reaction) with any of the components of the metal [17], and also they are not mutually soluble (or only to a smallest extent) [15, 16]. There are 130 ‘equilibrium’ values given in Table 3.
-
‘init.’: meaning the calculated value is just the initial contact angle, being valid within short contact times between the ceramic and the liquid metal; this category was chosen when chemical interaction [17] or significant mutual solubility [15-16] between the phases is expected, and thus the contact angle is expected to decrease with contact time. The equilibrium contact angle cannot be calculated by the equations presented in this paper. There are 158 ‘initial’ values given in Table 3.
As one can see from Table 3., the contact angle values vary within a relatively small interval, ranging from 143o for the Li/B4C system to 170o for the Pd/b
-SiC system. For the given liquid metal, the contact angle increases gradually in the following row: B4C à
Si3N4 à
b
-BN à
AlN à
a
-BN à
b
-SiC. The range of contact angle for one given metal decreases with the increasing average value of the contact angle. For Li, with a highest polarising effect the contact angle varies in the interval of 10o, while for Pd this interval is only 4o.
Finally we can conclude, that due to high surface tension of liquid metals, in absence of chemical interaction and mutual solubility between them and covalent ceramics, liquid metals never wet the surface of covalent ceramics better than 143o. This conclusion is in perfect agreement with our measured data [6-7], and also with the large number of experimental data obtained by other groups [1-5]. Although, it should be mentioned that there is a significant number of papers showing contact angle as low as 120o in non-reactive liquid metal / covalent ceramic phases. We presume that those experimental data probably refer to ceramics or liquid metals of oxidised surface. As oxides have ionic character, the new type of interaction, the ion-induced-dipole interaction becomes possible, ensuring higher adhesion energy and lower contact angle in the system (see [19, 9]).
Conclusions
Contact angle values have been estimated by the model developed by us earlier for non-reactive liquid metal / covalent ceramic systems. Among the 288 systems studied, 130 systems can be taken as ‘non-reactive’, i.e. the calculated value in this paper is expected to be an equilibrium value, being independent of contact time. In 158 systems some chemical reaction or mutual solubility in the system is expected, and so the calculated values will be valid in reality only during short contact times.
The calculated contact angle values vary within a relatively small interval, ranging from 143o for the Li/B4C system to 170o for the Pd/b
-SiC system. For the given liquid metal, the contact angle increases gradually in the following row: B4C à
Si3N4 à
b
-BN à
AlN à
a
-BN à
b
-SiC. The range of contact angle for one given metal decreases with the increasing average value of the contact angle. For Li, with a highest polarising effect the contact angle varies in the interval of 10o, while for Pd this interval is only 4o.
The effect of temperature has been found negligible in all systems (changing in the interval between +1o and –3o while the temperature changes by 100 K).
Finally it is concluded, that due to high surface tension of liquid metals, in absence of chemical interaction and mutual solubility between them and covalent ceramics, liquid metals never wet the surface of covalent ceramics better than 143o.
Table 3. Results of calculations (for the meaning of ‘eq.’ and ‘init’ see the text above)
|
Me |
Si3N4 |
b
-SiC |
B4C |
AlN |
a
-BN |
b
-BN |
|
Q
|
Type |
Q
|
Type |
Q
|
Type |
Q
|
Type |
Q
|
Type |
Q
|
Type |
|
Li |
145 |
Init. |
153 |
init. |
143 |
eq. |
148 |
init. |
148 |
eq. |
146 |
eq. |
|
Na |
149 |
eq. |
155 |
eq. |
146 |
eq. |
151 |
eq. |
152 |
eq. |
149 |
eq. |
|
K |
150 |
eq. |
155 |
eq. |
146 |
eq. |
152 |
eq. |
153 |
eq. |
151 |
eq. |
|
Rb |
152 |
eq. |
156 |
eq. |
148 |
eq. |
153 |
eq. |
154 |
eq. |
152 |
eq. |
|
Cs |
152 |
eq. |
155 |
eq. |
148 |
eq. |
153 |
eq. |
154 |
eq. |
152 |
eq. |
|
Be |
153 |
Init. |
161 |
init. |
154 |
eq. |
156 |
init. |
156 |
eq. |
154 |
eq. |
|
Mg |
159 |
Init. |
164 |
init. |
158 |
eq. |
161 |
init. |
161 |
eq. |
160 |
eq. |
|
Ca |
159 |
Init. |
163 |
init. |
157 |
eq. |
160 |
init. |
161 |
eq. |
159 |
eq. |
|
Sr |
161 |
Init. |
164 |
init. |
158 |
eq. |
162 |
init. |
162 |
eq. |
161 |
eq. |
|
Ba |
158 |
Init. |
162 |
init. |
156 |
eq. |
159 |
init. |
160 |
eq. |
158 |
eq. |
|
Al |
163 |
Init. |
167 |
init. |
162 |
eq. |
164 |
init. |
165 |
init. |
163 |
init. |
|
Ga |
157 |
Init. |
163 |
eq. |
157 |
eq. |
160 |
init. |
160 |
init. |
158 |
init. |
|
In |
162 |
eq. |
166 |
eq. |
161 |
eq. |
164 |
eq. |
164 |
eq. |
163 |
eq. |
|
Tl |
164 |
eq. |
167 |
eq. |
163 |
eq. |
165 |
eq. |
166 |
eq. |
164 |
eq. |
|
Si |
159 |
Init. |
165 |
init. |
159 |
init. |
162 |
init. |
162 |
init. |
160 |
init. |
|
Ge |
157 |
init. |
163 |
init. |
157 |
eq. |
160 |
init. |
160 |
eq. |
158 |
eq. |
|
Sn |
161 |
eq. |
165 |
eq. |
160 |
eq. |
163 |
eq. |
163 |
eq. |
161 |
eq. |
|
Pb |
165 |
eq. |
168 |
eq. |
164 |
eq. |
166 |
eq. |
166 |
eq. |
165 |
eq. |
|
Sb |
159 |
eq. |
164 |
eq. |
158 |
eq. |
161 |
init. |
161 |
eq. |
160 |
eq. |
|
Bi |
165 |
eq. |
168 |
eq. |
163 |
eq. |
166 |
eq. |
166 |
eq. |
165 |
eq. |
|
Cu |
160 |
Init. |
165 |
init. |
160 |
init. |
162 |
init. |
162 |
init. |
161 |
init. |
|
Ag |
161 |
Init. |
165 |
init. |
160 |
eq. |
163 |
init. |
163 |
eq. |
161 |
eq. |
|
Au |
164 |
Init. |
168 |
init. |
163 |
eq. |
165 |
init. |
165 |
eq. |
164 |
eq. |
|
Zn |
159 |
eq. |
164 |
eq. |
158 |
eq. |
161 |
init |
161 |
eq. |
159 |
eq. |
|
Cd |
162 |
eq. |
166 |
eq. |
161 |
eq. |
163 |
eq. |
163 |
eq. |
162 |
eq. |
|
Hg |
163 |
eq. |
167 |
eq. |
162 |
eq. |
164 |
eq. |
164 |
eq. |
163 |
eq. |
|
La |
159 |
eq. |
163 |
init. |
157 |
init. |
160 |
init. |
161 |
eq. |
159 |
eq. |
|
Ti |
160 |
Init. |
165 |
init. |
160 |
init. |
162 |
init. |
162 |
init. |
161 |
init. |
|
Zr |
162 |
Init. |
166 |
init. |
161 |
init. |
163 |
init. |
163 |
init. |
162 |
init. |
|
Hf |
162 |
Init. |
166 |
init. |
162 |
init. |
164 |
init. |
164 |
init. |
163 |
init. |
|
V |
159 |
Init. |
165 |
init. |
159 |
init. |
162 |
init. |
162 |
init. |
160 |
init. |
|
Nb |
161 |
Init. |
166 |
init. |
161 |
init. |
163 |
init. |
163 |
init. |
161 |
init. |
|
Ta |
163 |
Init. |
167 |
init. |
163 |
init. |
165 |
init. |
165 |
init. |
163 |
init. |
|
Cr |
157 |
Init. |
163 |
init. |
157 |
init. |
159 |
init. |
159 |
init. |
158 |
init. |
|
Mo |
162 |
Init. |
167 |
init. |
162 |
init. |
164 |
init. |
164 |
init. |
162 |
init. |
|
W |
163 |
eq. |
168 |
init. |
163 |
init. |
165 |
init. |
165 |
init. |
164 |
init. |
|
Mn |
157 |
Init. |
163 |
init. |
157 |
init. |
159 |
init. |
159 |
init. |
158 |
init. |
|
Re |
165 |
Init. |
169 |
init. |
165 |
init. |
166 |
eq. |
166 |
init. |
165 |
init. |
|
Fe |
160 |
Init. |
165 |
init. |
160 |
init. |
162 |
init. |
162 |
init. |
161 |
init. |
|
Ru |
162 |
Init. |
167 |
init. |
162 |
init. |
164 |
eq. |
164 |
init. |
163 |
init. |
|
Os |
164 |
Init. |
168 |
init. |
164 |
eq. |
166 |
eq. |
166 |
eq. |
164 |
eq. |
|
Co |
161 |
Init. |
166 |
init. |
161 |
init. |
163 |
init. |
163 |
init. |
161 |
init. |
|
Rh |
163 |
eq. |
167 |
eq. |
163 |
eq. |
164 |
eq. |
165 |
eq. |
163 |
eq. |
|
Ir |
164 |
eq. |
169 |
eq. |
165 |
eq. |
166 |
eq. |
166 |
eq. |
165 |
eq. |
|
Ni |
161 |
Init. |
166 |
init. |
161 |
init. |
163 |
init. |
163 |
init. |
161 |
init. |
|
Pd |
166 |
Init. |
170 |
init. |
166 |
init. |
168 |
init. |
168 |
init. |
167 |
init. |
|
Pt |
164 |
Init. |
169 |
init. |
164 |
init. |
166 |
init. |
166 |
init. |
165 |
init. |
References
-
Yu.V.Naidich, “Wettability of solids by liquid metals”, Progress in Surface and Membrane Science, 14 (1981), 353-492.
-
N.Eustathopoulos, M.G.Nicholas and B.Drevet, Wettability at high temperatures (Pergamon, Amsterdam, 1999).
-
Proceedings of the International Conferences on High Temperature Capillarity, ed. by N.Eustathopoulos, #1, Reproprint, Bratislava, Slovakia, 1995, #2, (co-editor: N.Sobczak), Foundry Research Institute, Cracow, Poland, 1998, #3, to be published in 2001 by the Welding Institute of Japan.
-
G.Kaptay, E.Báder, L.Bolyán, “Interfacial Forces and Energies Relevant to Production of Metal Matrix Composites”, Materials Science Forum, 329-330 (2000), 151-156.
-
Databank on Contact Angle Data – Appendix to the PhD Thesis of E.Báder, University of Miskolc, 2000
-
L.Zoltai, E.Bader, G.Kaptay, P.Arato, Proc. of Microcad ’2000, Section B: Materials Technology, University of Miskolc, 2000, pp. 121-126.
-
E.Báder, L.Zoltai, M.Hördler, P.Arató, R.F.Singer, G.Kaptay, to be published in: “Proc. of 3rd International Conference on High Temperature Capillarity HTC-2000, Kurashiki, Japan”, in 2001
-
G.Kaptay, L.Zoltai, E.Báder, to be published in Proc. of Microcad 2001, 6 pages.
-
E.Báder, see this issue
-
T.Iida, R.I.L.Guthrie: The Physical Properties of Liquid Metals, Clarendon Press, Oxford, 1993.
-
T.Ja. Kosolapova: Svoistva, poluchenie i primenenie tugoplavkih soedinenii. Metallurgia, Moskva, 1986
-
J.Emsley: The Elements - Clarendon Press, Oxford. 1989
-
CRC Handbook of Chemistry and Physics, ed. by D.R.Lide, CRC Press, 1993-94
-
T.M.Miller, B.Bederson: Advances in Atomic and Molecular Physics, 13 (1977) 1
-
Alloy Phase Diagrams, ASM Handbook vol. 3. ed. by H. Baker, 1992
-
T.B.Massalski, et al.: Binary Alloy Phase Diagrams, 2nd ed., ASM Int., Materials Park, OH., 1990
-
I.Barin: Thermochemical Data of Pure Substances – WCH, 1993.
-
A.I. Efimov: Properties of Inorganic Compounds (in Russian) – Khimiia, Leningrad, 1983.
-
G.Kaptay, E.Báder, to be published in: “Proc. of
3rd International Conference on High Temperature Capillarity HTC-2000”, Kurashiki, Japan, in 2001
-
G.Kaptay, Interfacial Energies and Phenomena in Metallurgical and Materials
Technologies (in Hungarian), Thesis for dr. habil, Miskolc, 1998 (61
pp)
-
G.V.Samsonov, I.M.Vinickii, Refractory Compounds
(in Russian), Metallurgiia, Moscow,1976
|


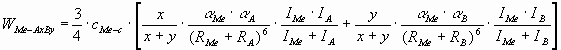 (1)
(1)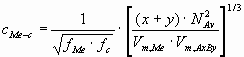 (2)
(2)