|
|
Kezdőlap-Home
Page |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
II. évfolyam 3. szám 2001. július [HUN] - Magyar cikk
|
Estimation of the absolute values of cohesion energies of pure metals G.Kaptay, G.Csicsovszki, M.S.Yaghmaee, LIMOS R&D, Department of Physical Chemistry,
1. Introduction Cohesion energy (or binding energy) is a basic energetic property of metals, influencing the majority of their other physical properties. The cohesion energy of solid and liquid metals is the energy connecting atoms in the solid and/or liquid state. Although the usefulness of the concept of cohesion energy is obvious for both education and research, its concept is used less than expected. The major reason for that is that there are no straightforward experimental or theoretical methods to obtain the absolute value of the cohesion energy. This is mainly due to the fact, that chemical thermodynamics works with relative, not absolute values. Although any change in the state of the matter is perfectly described by the (relative) Gibbs energy change accompanying this process, the cohesion energy in pure metals would require an absolute scale. In the present paper this question will be discussed, and some preliminary results will be presented.
2. The State of the Art of the Problem of Cohesion Energy in Metals According to chemical thermodynamics, the heat of formation of pure elements in their most stable state is taken equal zero, by definition. Thus, the heat of formation of all solid metals (and liquid mercury) is zero by definition, at 298.15 K and at 1 bar. Consequently, the ideal gas of all metals at 298.15 K and at 1 bar is characterised by some positive values of the heat of formation. Therefore, using formal logic, the heat of sublimation of metals should be characteristic to the energy of broken bonds in the solid or liquid phase, as in ideal gas (by definition) such bonds between gaseous atoms do not exist. Therefore, the classical equation to calculate the cohesion energy in metals at 0 K can be written as:
where D fH° g(0K) - the enthalpy of formation of gaseous metals at 0 K (kJ/mol), D fH° s(0K) - the enthalpy of formation of solid metals at 0 K (kJ/mol). Eq.(1) is recognised by the scientific community in a contradictory way. On the one hand, it is often used as a correlation parameter for different physical properties in the scientific literature (see for example [1]). On the other hand, in the textbooks on materials science cohesion energy or binding energy in metals is usually considered only qualitatively, without the values of the binding energies [2-8], or with only some examples of binding energies [2, 7] (the situation is similar in textbooks on physical chemistry [9-10]). However, the various properties of metals are described mostly in a phenomenological way, without an attempt to make the bridge between them, using the concept of cohesion (binding) energies. Is the activation energy of diffusion in solid metals connected with the surface energy of metals ? Are both of these quantities connected with the energy of vacancy formation ? The answers to these questions are YES, and the same answer can be given to many similar questions, as well. The key is the cohesion energy, connecting different properties of the same material. Of-course, professors worldwide should not be blamed that the scientific description of the discipline called materials science has not been written yet, or that this task is passed to quantum mechanics (which is unable to give consumable explanations to ordinary students on materials science). It should be recognized, that the concept of cohesion energy is not matured yet, and that is why at this moment it is not ready to be involved in textbooks. Today it would rather confuse, than clear the minds of the students. It should also be mentioned that the concept of cohesion energy is discussed in some of the aforementioned textbooks, in relation to ionic crystals, where the concept has been found more useful in explaining certain trends in properties of this class of materials. It is also important to remember, that for ionic crystals the definition of the cohesion energy is more sophisticated than that given by Eq.(1). Moreover, the values of cohesion energy calculated from the thermodynamic Born-Haber cycle is in fairly good agreement with calculations based on a simplest energetic model of ionic crystals (the Coulomb energy). Such a nice connection is also missing in the world of metals. Missing a simple and widely known solution to a problem today, however, does not mean that the problem cannot be solved, or that the concept of cohesion energy in metals would not have sense, or value. It is probably accepted by all who works in materials science of metals that at given T and p all metals with known composition and structure possess a unique, absolute value of the cohesion energy, and this value largely determines various mechanical, thermochemical, transport, etc. properties of metals. Thus, the impossibility to measure or calculate these values is indeed frustrating. One of the possible and elegant ways ‘around the problem’ is to scale the cohesion energy by some macroscopic properties of the material [11-12], such as melting point and molar volume at 0 K (and at 0 Pa). Although the absolute values of the cohesion energies are lost in this way, the potential to apply the concept of cohesion is saved, using a relative scale. The goal of this paper is to show the reasons why the classical definition Eq.(1) of the cohesion energy fails for metals, and also to try to give in first approximation an absolute scale for cohesion energy of metals. The authors realise that the subject is very much controversial, and also that the table of absolute cohesion energies of metals to be suggested in this paper is not the final, and not the most perfect table for this property. However, we think that this subject is vital for our education efficiency and also for basic research, and therefore it is worth to talk about, even if criticism is expected.
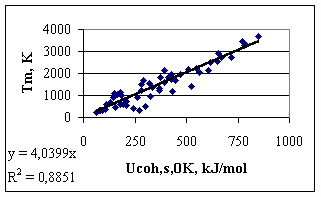
3. The reasons of imperfection of Eq.(1) as definition for cohesion energy of metals Eq.(1) as definition for the cohesion energy in pure metals would be perfect, if metallic atoms of different elements would be in the same energetic situation in a 1 bar ideal gas. At first sight, it is the case, as in the ideal gas, by definition, all interactions between atoms are negligible. However, the stability of gaseous atoms themselves of different elements are different, due to the different stability of their outer electron shells. For example, the vapour of Mg (with a relatively stable s2 configuration) is much more stable than the vapour of Na (with an s1 configuration) or the vapour of Al (with an s2p1 configuration). This difference is reflected in an exceptional behaviour of Mg (and other s2 metals) in the general trends established between the cohesion energy (defined in a classical way) and different properties of metals. Let us present this controversies on the example of the dependence of the melting points of metals on cohesion energy defined by Eq.(1) (see Fig.1), especially that melting point was suggested and successfully applied by Beke et al [11-12] in correlation of some properties of metals. Data are taken from [13, 14]. One can see, that although there is an obvious correlation between the two quantities, the scatter in Fig.1 is quite large, with an R2 = 0.88. One can see, that two metals (Mg and Al), having practically the same melting points (923 and 933 K, respectively), differ in cohesion energy values significantly (-146 kJ/mol and -327 kJ/mol, respectively). Although the two metals differ also in crystal structure (hcp for Mg and fcc for Al), this would explain a difference of much less than 10 kJ/mol [13]. Therefore, the ‘contradiction’ is obviously explained by different electron structures of metals in the ideal gas. This is obvious also, if one compares the electron affinities of gaseous metals. For ‘normal’ metals withot extra stability of gaseous atoms the electron affinity has a negative value, while for metals with extra stable electron configuration in gaseous state the electron affinity is positive (Be, Mg, Ca, Sr, Ba, i.e. the s2 metals, Cd and Hg, i.e. the d10s2 metals, Sc and Y, i.e. the d1s2 metals, and Mn, i.e. the d5s2 metal [17]).
Fig.1. Melting points of metals as a function of their cohesion energy defined by Eq(1) 4. Physical Properties for Scaling the Cohesion Energy Our goal is to introduce corrections to the classical definition of the cohesion energy. For that, however, we need some property (preferably as many as possible independent properties), which surely will be proportional to the real cohesion energy. Moreover, we need at least one property, for which also the constant of proportionality is known, and hence our relative scale can be made absolute. One of the scaling parameters will be the melting point, as suggested earlier by Beke et al [11-12], and also by many researchers, searching for trends between properties of materials (see for example [1]). However, the theoretical ratio between the melting point and the absolute value of the cohesion energy is not known. The value of the slope in Fig.1 (-4.04) is considered as a purely empirical value. It should also be mentioned that among physical properties of solid metals it is hard to find a property, connected with the absolute cohesion energy with theoretically supported proportionality constant. The reason is that the properties of solid metals depend largely on structure and also structure imperfections, which make solid state physics a very complicated subject. On the other hand, the majority of these structure differences between different metals disappear upon melting. Although the crystal structure and long-term order is lost, all irregular imperfections and strains are lost, as well. Therefore, the structure and energetics of different liquid metals just above their melting points are much more similar to each other, even if the mathematical description of their structure is obviously more complicated than that of ideal (and therefore not real) solid crystals. For example, the average coordination number in all liquid metals just above their melting point is about 11 [1], although the experimental determination of this quantity is not very accurate. Nevertheless, large coordination differences, such as between bcc and fcc (or hcp) structures (8 against 12) disappear upon melting. As an example, let us remind the cases of Ge and Si, with 4-coordination and non-metallic properties in solid state, becoming true metals with the coordination of about 11 above their melting points. Therefore, we suggest to search an absolute scaling parameter for the cohesion energy in metals among the properties of liquid metals. If the cohesion energy in liquid metals is known, it can be easily extrapolated back to solid through the well known value of enthalpy of melting and heat capacity of solids. To our opinion, the best, theoretically supported correlation between the cohesion energy in liquid metals and their properties is provided by the surface tension of liquid metals. The enthalpy part of the surface tension (converted from J/m2 into the J/mol scale) characterises the certain ratio of the ‘broken bonds’ at the surface compared to bulk, i.e. the certain ration of the cohesion energy. This ratio depends on the structure of the bulk and surface liquid metals. If bulk liquid metals are taken with an average coordination number of 11 [1], and surface liquid metals are structured similar to the (111) plane of the fcc lattice with the surface coordination number 9, this ratio can be found theoretically. According to our earlier results [15,16], the following quantity should be proportional to the cohesion energy in the liquid metal at its melting point, with the proportionality constant of a = -0.172:
where s lg is the surface tension of liquid metals at their melting points (J/m2), Vm – is the molar volume of liquid metals at their melting points (m3/mol), NAv = 6.02 1023 mol-1 – the Avogadro number, Tm – the melting point of metals (K), the constant 0.001 is used to have the unit of Y in kJ/mol. The following relationship exists between the cohesion energy of liquid metals and the cohesion energy of solid metals at 0 K:
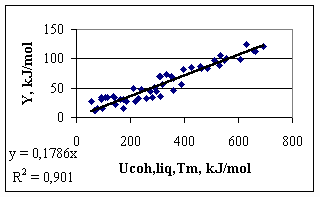
where Cp – is the heat capacity of solid, D mH – is the enthalpy of melting of the metal at its melting point. For metals with allotropic transformations between 0 K and Tm the heats of those transformations should also be added to Eq.(4). The correlation between parameter Y and the cohesion energy of liquid metals calculated by the classical definition (Eq.1) is presented in Fig.2. Values for surface tension and molar volume of liquid metals are taken from [1]. From Fig.2 one can see, that the correlation clearly exists, with R2 = 0.90, and with a similar to the theoretical (-0.172) average coefficient a = -0.179. Mg is again situated ‘out of the correlation’ (a = -0.298), due to the error in Eq.(1), i.e. due to the special electronic structure of gaseous Mg. The only problem with Fig.2 and with values for the surface tension of liquid metals is, that its measurement for many metals is difficult due to surface contamination by oxygen, and due to high temperatures. The correlation in Fig.2 is not perfect partly because of that, and partly because of Eq.(1).
Fig.2. Parameter Y as function of cohesion energy of liquid metals calculated by the ‘classical definition’
5. The absolute scale of Cohesion Energy In order to make the absolute scale for the cohesion energy of metals, the task will be solved in two steps:
First, a liquid ‘reference’ metal should be chosen, having the following properties:
Liquid gold has been chosen by us as a ‘reference metal’. It has an fcc structure with no allotropes at 1 bar, Tm = 1,338 K, Uocoh(s,0K) = -368.0 kJ/mol (see Eq.(1)) [13, 14], D Us,0K-l,Tm = 47.86 kJ/mol [13, 14], Uocoh(l,Tm) = - 320.14 kJ/mol, Vm = 11.3 10-6 m3/mol, s lg = 1.169 J/m2 [1], Y = 56.97 kJ/mol. Parameter a = -0.178, i.e. it is not far from the theoretical value. If the theoretical value of a = -0.172 is used, the corrected values for Au will be as follows: Uocoh(l,Tm) = - 331.2 kJ/mol, Uocoh(s,0K) = -379.1 kJ/mol. This value will be taken as the absolute cohesion energy of solid Au at 0 K. The theoretical proportionality constant between the melting point and the cohesion energy of the liquid at its melting point can be found from the value for gold as: 1,338 K / -331.2 = -4.04 Kmol/kJ. In the first approximation, the same slope can be used to find absolute values of cohesion energies of other liquid metals at their melting points, as well:
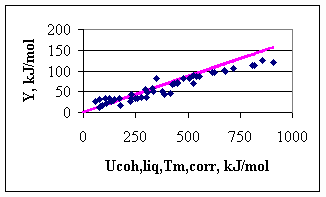
with Tm in [K] and Ucoh in [kJ/mol]. Once the cohesion energies for liquid metals are estimated by Eq.(5), the cohesion energies of solid metals can be re-calculated by Eq.(4). In this way, the cohesion energy of two solid metals with the same melting point, but different structures will be different, as the melting entropy (being the part of Eq.(4)) is a structure sensitive property. As an example, for Al one can find: Uocoh(l,Tm) = 933/-4.04 = -230.9 kJ/mol, Uocoh(s,0K) = -263.6 kJ/mol. This value is more positive by 20 %, compared to the classical value of -327 kJ/mol. For Mg: Uocoh(l,Tm) = 922/-4.04 = -228.2 kJ/mol, Uocoh(s,0K) = -259.6 kJ/mol. This value is more negative by 78 % compared to the classical value. Hence, the value for Mg with extra high stability of the gaseous atom was shifted to the negative direction much more, than the value of Al was shifted to the positive direction, with obviously somewhat higher than the average in-stability of gaseous atoms. In Fig.3 the dependence of parameter Y on the corrected values of the cohesion energy is shown. One can see that for low-cohesion energy metals the data points are situated around the ideal line (drawn with a slope of 0.172), with a scatter normal to surface tension of metals. For high cohesion energy metals, however, the ideal line is significantly above the measured points. This might be the indication that the surface tension of high melting point metals is still known with not a sufficient accuracy, due to difficulties of measurements and to the role of adsorbed oxygen.
Fig.3. Dependence of parameter Y on the corrected cohesion energy of the liquid metals (data points: experiment of [1], line: ideal line with the slope of 0.172)
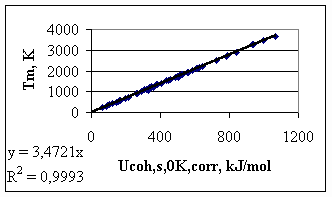
In Fig.4 the correlation between the corrected cohesion energy at 0 K for solid metals and the melting point is shown. The correlation is ‘too good’ (with R2 = 0.999), but this is due to Eq.(5). However, it can be seen that the scatter of maximum 5 kJ/mol is still present, due to the structural differences between different solid metals. From Fig.4 one can see that any correlation given in the literature between properties of metals and their melting point, can be converted into the more sensible correlation between those properties and the cohesion energy in metals. The ‘theoretical’ proportionality constant of –3.5 ± 0.3 has been established between the melting point and the cohesion energy of solid metals at 0 K (see Fig.4).
Fig. 4. Correlation between the corrected cohesion energy values of solid metals at 0 K and melting point of metals In Table 1 the suggested values for the cohesion energies of solid metals at 0 K and liquid metals at their melting point are collected. It is suggested to use these tables to search for correlations between different properties of metals and cohesion energy. Empirical constants found in this way between different properties and the cohesion energy can be rationalised and compared with ‘absolute’ theories.
Table 1. The suggested values of absolute cohesion energies of metals
Conclusions In the present paper the reasons why the sublimation energy of metals cannot be a proper estimation for the absolute cohesion energy in metals are discussed. The table of absolute cohesion energies of pure solid and liquid metals has been constructed, based on the surface tension of liquid gold, as a ‘reference value’. The melting point of metals was used as an another correlation parameter. It is suggested to use these tables to search for correlations between different properties of metals and the cohesion energy. Empirical constants found in this way between different properties and the cohesion energy can be rationalised and compared with ‘absolute’ theories. This method is suggested to use in education and in basic research.
Acknowledgements The authors are grateful for prof. P.Bárczy of the University of Miskolc and to prof. D.Beke of the University of Debrecen for their helpful discussions of the matter discussed in this paper.
References
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

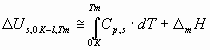 (4)
(4)