|
Introduction
The daily characterisation of steel microstructures is usually made by comparing the microstructure with reference pictures of the different standards. This procedure is enough for routine measurements but for research and product development it is important to find much more powerful methods. The development of image analysers have made possible to measure a lot of feature parameters but it is not easy to find the appropriate expression of these parameters that is the most adequate in the case of a given microstructure. After introducing the most frequently used morphological expressions we will show the results of some comparative investigations in normalising rolled and thermomechanically rolled samples to find out the efficiency of these expressions. In this paper the characterisation of the ferrite phase will be discussed.
Measured stereological parameters
The most frequently used measured ferrite grain section (feature) parameters are as follows:
Area (A): the total number of detected pixels within the feature.
Convex area (ConvexA): the area of the polygon circumscribing the feature, formed by tangents to its boundary.
Perimeter (P): the total length of the boundary of the feature.
Convex perimeter (ConvexP): The length of the polygon circumscribing the feature, formed by tangents to its boundary. This is similar to the length of a piece of string stretched around the feature.
Length (L): the length of the longest tangent diameter.
Breadth (B): the length of the shortest tangent diameter.
Derived shape factors
From these measured parameters several shape factors can be derived to describe the shape of the ferrite grains. Usually these shape factors are dimensionless quantity, independent from the size of the grains and their position. Since the shape of the ferrite grains is usually globular, we have selected three shape parameters that give a special value, 1 in the case of circular grain cross-sections.
The used shape factors to describe the shape of the ferrite grain cross-sections are as follows [1,2,3]:
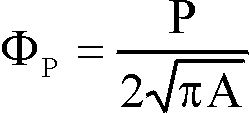 (1) (1)
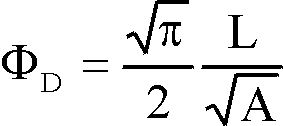 (2) (2)
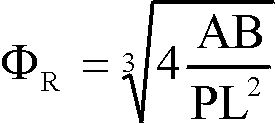 (3) (3)
Equation 1 and 2 are derived from geometrical basic data, Equation 3 is derived from geometrical inequation. Two additional parameters, (Area/Convex Area)1/2 and (Perimeter/Convex Perimeter) can show the convexity of the grain cross-sections as well. Their value is 1 for circular cross-sections.
Shape vectors can be easily derived from the three shape factors:
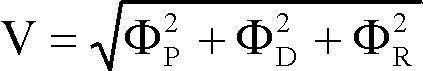 (4) (4)
Image analysing
To evaluate the usefulness of the parameters described above in the case of normalising rolled and thermomechanically rolled steel wide strips we carried out a comparative measurement. Four samples were selected for the metallographical investigation. Characteristic pictures of the samples are shown in Figure 1-4. Two of the samples were normalising rolled (sample VA2 and KA2), the other two (sample 5B and 1H) were thermomechanically rolled. We measured the presented stereological parameters by image analyser on microscopic images. More than ten thousand grain cross-sections were measured on each sample, the result of the measurement can be seen in Table 2. The calculated shape factors are listed in Table 3.
It can be seen that the grain sizes of the samples produced in the two different ways are rather different, but the shape factors are independent from the size of the grains as stated above. There is a significant difference in the shape factors and the shape vector of the samples produced by the two rolling technologies. The so-called circularity measure (F
P) shows the largest difference between the four samples. According to the value of the (Area/Convex Area)1/2 and (Perimeter/Convex Perimeter) parameters the convexity of the normalising rolled samples is a little bit larger than the convexity of the thermomechanically rolled samples.
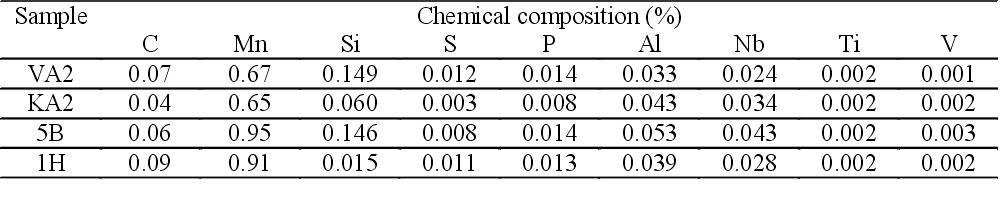
Table 1. Chemical composition of the samples
|

|

|
|
Figure 1
Sample VA2, 500x, Nital |
Figure 2
Sample KA2, 500x, Nital |
|

|

|
|
Figure 3
Sample 5B, 500x, Nital |
Figure 4
Sample 1H, 500x, Nital |
Table 2. Measured stereological parameters
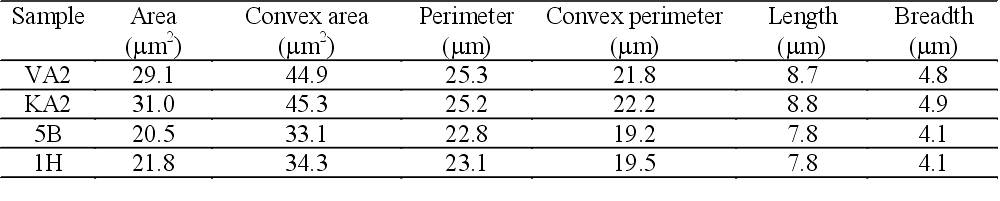
Table 3. Shape factors

The chemical composition and the production technology of these four samples were rather different and the resulting large variety of the microstructures was advantageous when we wanted to evaluate the usability of the morphological parameters. Since the grain structure and the mechanical properties depend on the composition and the production technology, in these cases we could not find a correlation between the grain structure and the mechanical properties.
For further investigations tensile test specimens machined from the same plate were heat treated. The aim of the heat treating was the production of samples with different microstructure but with the same chemical composition. The duration of the heat treating was 25 minutes, the temperature was 700°
C (sample No. 91, 92), 750°
C (No. 93, 94), 800°
C (No. 95, 96), 850°
C (No. 97, 98) and 900°
C (No. 99, 100). The samples were cooled in air. The chemical composition of the samples can be seen in Table 4., two characteristic microstructures are shown in Figure 5. and Figure 6. The microstructure of the samples is ferritic/pearlitic. The measured stereological parameters of the ferrite grains are in Table 5., the shape factors and yield stress values are in Table 6.
From the measured parameters it can be stated, that larger heat treating temperature means smaller ferrite grains. Despite of the large size changing during heat treating there is only a little variation between the shape of the ferrite grain cross-sections. The values of the shape factors are a little bit closer to one after heat treating at larger temperatures, that is their shape is closer to the circular shape.
Multiple regression was carried out to investigate the correlation between the microstructure and the yield stress. The evaluation is based on the well-known fact that the yield stress is directly proportional to the volume fraction of the different phases of the multiphase structure and is inversely proportional to the square root of the linear dimension of the grains. In the regression equations grain specific volume was used instead of the invert linear dimension having regard to the grain shape. Several similar equations were tested and we found that the optimal equation – when the regression coefficient is close to one and there is a real physical meaning – is as follows (see Figure 7.):
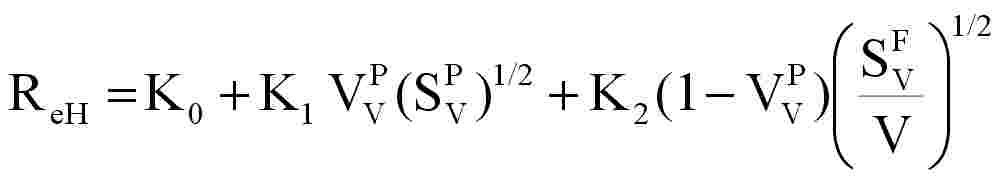 (5) (5)
where K0»
0
K1=365.4
K2=492.2
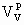 = perlite volume fraction = perlite volume fraction
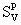 = perlite surface in volume = perlite surface in volume
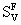 = ferrite surface in volume = ferrite surface in volume
V= length of the shape vector.
Table 4. Chemical composition of the heat treated samples

|

|

|
|
Figure 5
Sample 90, 500x, Nital |
Figure 6
Sample 100, 500x, Nital |
Table 5. Measured stereological parameters
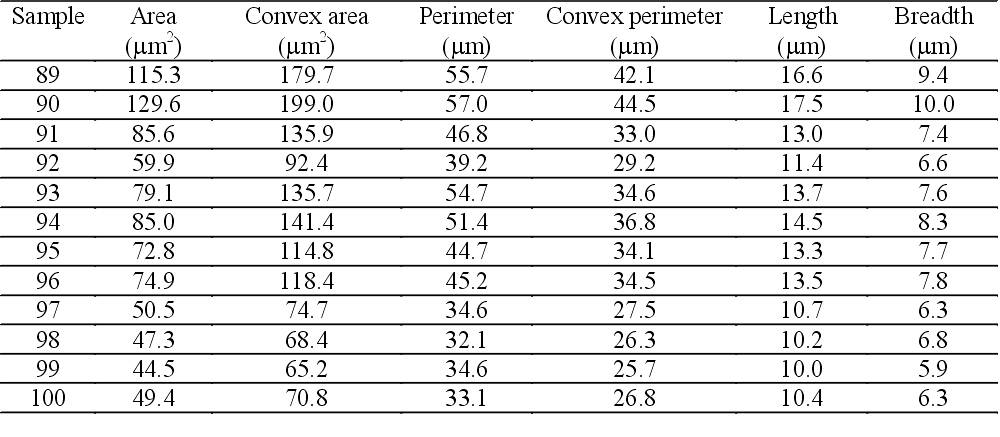
Table 6. Shape factors and yield stress
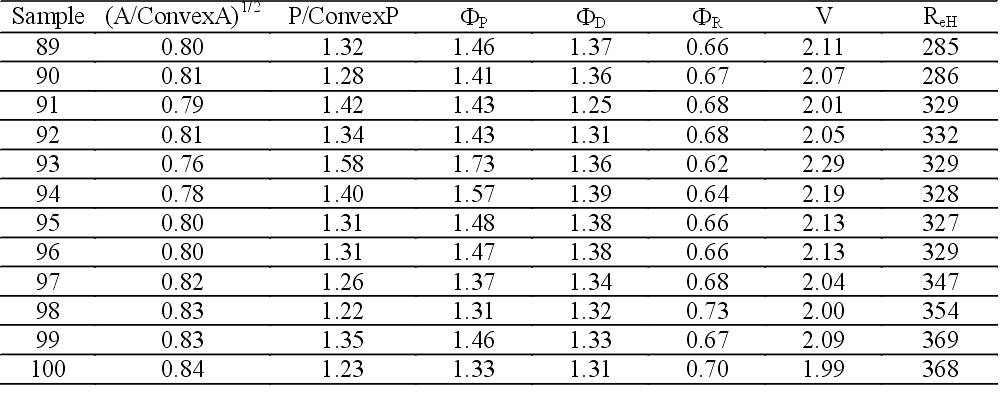
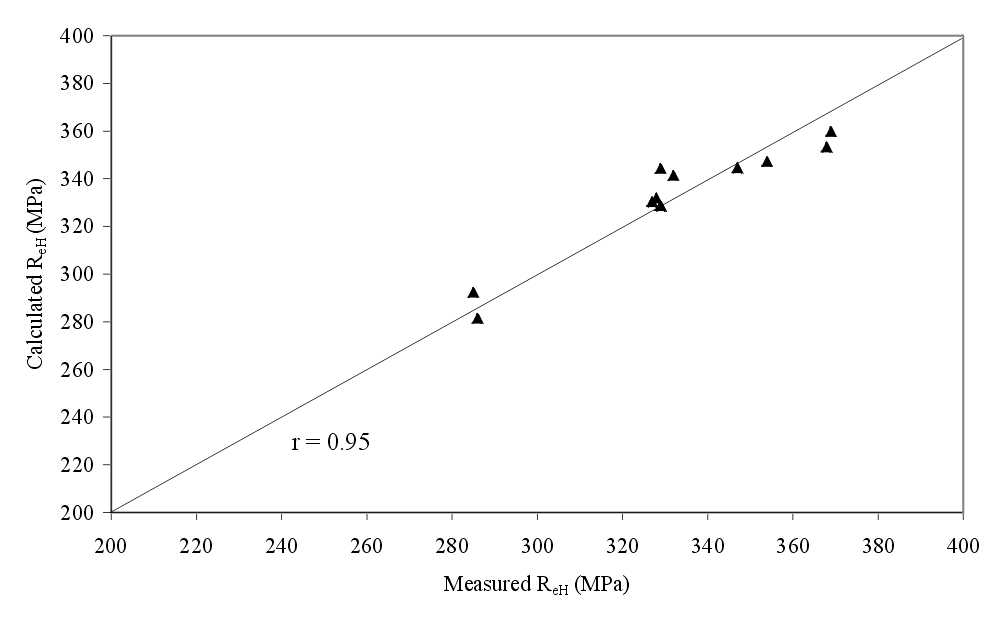
Figure 7
Measured and calculated yield stress values
Conclusions
Stereological investigations were carried out to describe the microstructure of normalising rolled and thermomechanically rolled steel wide strips and to find a correlation between the microstructure and the mechanical properties of a ferritic/pearlitic steel. The measured parameters and the calculated morphological factors were appropriate for the classification of the ferrite grains after controlled temperature rolling. Nevertheless we found that for the best result several different shape factors of the ferrite grains have to be measured. The studied ferritic/perlitic microstructure can be properly characterised by the surface in volume of the two phases and the described shape vector of the ferrite grains.
Acknowledgements
The authors would like to acknowledge the support from the Bolyai Janos Research Scholarship of the Hungarian Academy of Sciences.
References
1) W. K. Pratt, Digital Image Processing, John Wiley and Sons, New York, (1987), p. 525-534
2) J. R. Parker, Practical Computer Vision Using C, John Wiley and Sons, New York, (1994)
3) L. A. Santalo, Integral Geometry and Geometric Probability, Addision-Wsley, Reading, Massachusetts, (1976)
4) E. E. Underwood, Quantitative stereology, Addison-Wesley Publishing Company, California (1970)
5) Y. Bergström and H. HallEn, Metal Sci 17, (1983), p. 341-347
|

