Maziar S.Yaghmaee1, György Kaptay2, Gyula Jánosfy3 1-2 LIMOS Research Group, Department of Physical Chemistry 3 LIMOS Research Group, Department of Ferrous Metals 1-3University of Miskolc, Faculty of Metallurgy, HU-3515 Miskolc-Egyetemváros, Hungary Introduction During solidification of steels containing nitrogen and boron the precipitation of the BN and Fe2B phases are also expected correspondingly inside and along the austenite grain boundaries. Their influence on the mechanical properties of the steel has stimulated our research program to study the forms of existence of B and N in liquid steel and the solubility of BN and N2 gas in the liquid phase of the ternary Fe-B-N system. For this reason, the model of an ideally associated mixture has been applied on the liquid phase of the ternary Fe-B-N system. A similar treatment of the same authors for the Fe-Al-N system has been recently published [1]. The Model of an Ideally Associated Mixture for the Liquid Phase of the Ternary Fe-B-N System The basic concept of the model of an ideally
associated mixture is that the major part of interaction
between the components is consumed through the formation
of associates (molecules) in the liquid phase (see [2-3]),
while the mixture of associates and the monomers are
treated as an ideal solution. Major associates to be
taken into account in the Fe-rich corner of the liquid
phase of the ternary Fe-B-N system are Fe2B
and BN. In equilibria, the associates Fe2B and
BN are in chemical equilibrium with monomers (i.e.
components not bonded into associates) called Fe1,
B1 and N1. Note the difference
between components of the melt Fe, B, N and the model
monomers Fe1, B1 and N1.
For the model, 1 mole of the Fe, B and N atoms will be
considered (nFeo + nBo
where nS = nFe1 + nB1 + nN1 + nFe2B + nBN; KFe2B and KBN are the equilibrium constants of reactions of formation of Fe2B and BN from gBN is the activity coefficient of the BN molecules dissolved in liquid iron. It can be shown, that the thermodynamic activity, a, of the macroscopic components is equal to the mole fraction of model monomers [2-3], i.e. the following equations hold:
Model Parameters The system of equations (1-5) can be solved for various macroscopic compositions of the melt (i.e. for given concentrations of B and N) at different temperatures. For this purpose, the equilibrium constants of reactions of the Fe2B and BN formation need to be known. Considering the value –67.87 kJ/mol suggested by [4] for the heat of formation of Fe2B and combining it with the entropy of formation (16.045 J/molK at 1900 K) given by [5] the final equation for KFe2B can be written as:
The temperature dependence of the equilibrium constant of the reaction 0.5 N2 + B = BN is expressed by [5]:
However, nitrogen in liquid steel is dissolved as a monomer, and therefore, Eq.(8) needs to be corrected accordingly. The solubility of nitrogen (at 1 bar pressure of nitrogen) in pure liquid iron [6] is:
From Eq (9.a) the solubility of nitrogen, as a function of the partial pressure of nitrogen (in bar), in pure iron [6] can be expressed as:
Eq.(9.b) is used later to determine the phase boundary between the liquid phase of the ternary Fe-B-N system and N2 gas phase at a particular pressure of nitrogen and constant temperature. The activity coefficient of N atoms in liquid steel is the inverse of its solubility. Hence, combining Eq-s (8-9.a), the final equation describing the equilibrium constant of the reaction [N] + B = BN can be written, as:
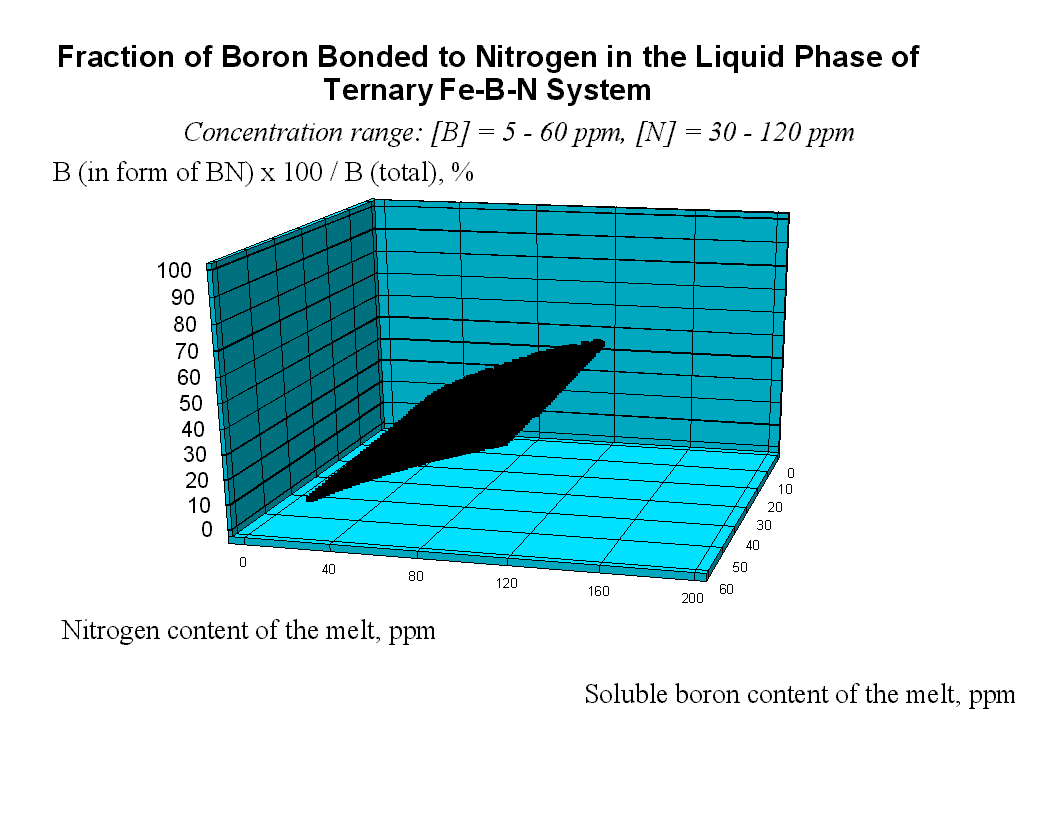
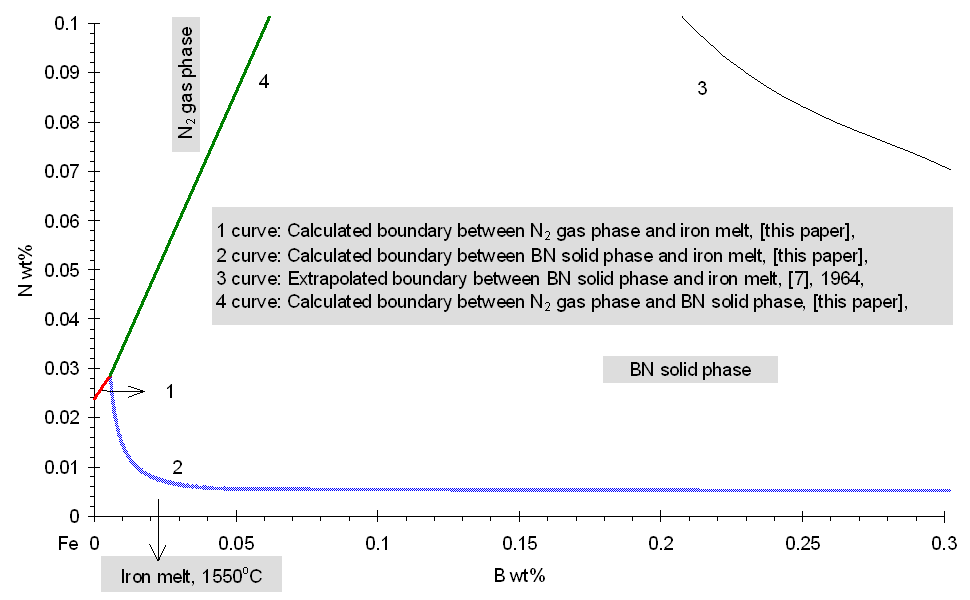
Boron and Nitrogen in Liquid Steel The system of equations (1-5) was solved using the model parameters described by equations (7, 10) for different compositions of steel at different temperatures. The fraction of boron existing in the form of BN associates is shown in Fig.1. One can see that when the nitrogen content of the melt reaches the value of 80 ppm, more than 37 % of the boron is in the form of BN associates. As the soluble boron content of the melt varies from 5 to 60 ppm this percentage goes down by only 7 % which is true also for the other nitrogen levels. The remaining part of boron which is around 61 % of the total B, is bonded to Fe as Fe2B and only a minor part of boron is atomically dissolved in the melt. As the boron content of the melt reaches the value of 50 ppm at nitrogen level of 30 and 120 ppm, respectively more than 30.5 % and 22.8 % of nitrogen is in the form of BN associates. Computation of Phase Equilibria The solubility of N2 gas (at 0.27 bar pressure of nitrogen) in the liquid phase of the ternary Fe-B-N system has been calculated combining our model (See Eq.(1-5).) with Eq.(9.b). The result is shown by curve 1 in Fig.3. One can see that the solubility of N2 increases with increasing B content of the melt, due to formation of BN associates that decrease the activity of N in the liquid steel. In order to calculate the equilibrium between the liquid phase of the ternary Fe-B-N system and the solid BN phase, the integral Gibbs free energy of the liquid phase of the ternary Fe-B-N system is described as:
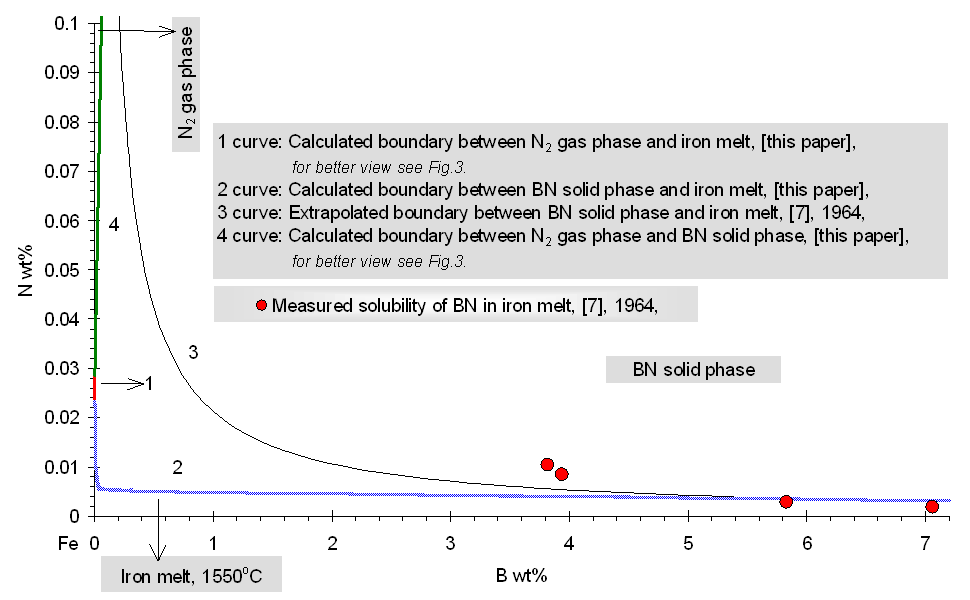
where R: universal gas constant, 8.314 J/molK; T: absolute temperature, [K]; Gl: integral Gibbs free energy of the liquid phase of the ternary Fe-B-N system, [J/mol]. According to general condition of heterogeneous equilibrium, the concentrations of N and B in liquid iron being in equilibrium with the solid BN phase has been calculated by using an in-house computer program called PHILOMATH. The Gibbs energy of formation of pure BN is derived from Eq.(8). From this procedure, the solubility of solid BN in the liquid phase of the ternary Fe-B-N system is found. Results of calculations are shown by curve 2 in Fig.2-3. for high and low boron containing melts, alike. Fig. 1. The fraction of boron bonded in BN associates in the liquid phase of the ternary Fe-B-N system at 1823 K Comparison of Previously Published Data and Model Results The phase boundary between the liquid phase of the ternary Fe-B-N system and the solid BN phase at 1823 K is shown by curve 2 in Fig.2-3. The same phase boundary is shown by curve 3, according to the literature [7]. Curve 3 is drawn based on measured values with a B content varying from 3.82 to 7.06 wt%. One can see, that our calculated results fit well those experimental data of [7] in Fig.2. By setting the value of gBN to be 10, we were able to fit the model result to the measured points. However, if data of [7] are extrapolated to other concentration regions (that is, lower boron) then, as one can see from Fig.2-3., there is a strong deviation from our model results, which may only be attributed to the misleading concept of solubility product that ignores complex formation in the liquid. This means, that the concept of the "solubility product" fails, if strong complex formation takes place in liquid metals.
Fig. 2. Fe-rich corner of the Fe-B-N system at 1823 K, compared with previously published data at high boron concentration Conclusions
Fig. 3. Fe-rich corner of the Fe-B-N system at 1823 K, compared with previously published data at low boron concentration References [1] M.S. Yaghmaee, G. Kaptay, G. Jánosfy: Materials Science Forum Vols. 329-330 (2000) pp. 519-524 [2] K.Wasai, K.Mukai: J.Japan Inst.Met., 46 (1982) p. 226 [3] G.Kaptay, E.Berecz: Chemical Papers, 45 (1991) p. 145 [4] S.Sato, O.J.Kleppa: Met.Trans B., 13B (1982) 251 [5] I. Barin: Thermochemical Data of Pure Substances, VCH Verlagsgesellschaft mbh, Weinheim, 1993 [6] E.T.Turkdogan: Fundamentals of Steelmaking, The Institute of Materials, London, (1996) [7] D. B. Evans-R. D. Pehlke, Trans AIME, 230, (1964). pp. 1657-1662. Copyright © 2000 |
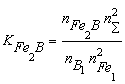 (4)
(4)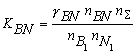 (5)
(5)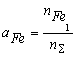 (6.a)
(6.a)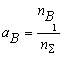 (6.b)
(6.b)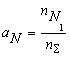 (6.c)
(6.c)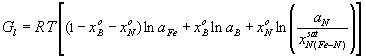 (11)
(11)